Bayesian Random-Effects Meta-Analysis

Bayesian meta-analysis assuming that the effect size \(d\) varies across studies with standard deviation \(\tau\) (i.e., a random-effects model).

meta_random(
  y,
  SE,
  labels,
  data,
  d = prior("cauchy", c(location = 0, scale = 0.707)),
  tau = prior("invgamma", c(shape = 1, scale = 0.15)),
  rscale_contin = 0.5,
  rscale_discrete = 0.707,
  centering = TRUE,
  logml = "integrate",
  summarize = "stan",
  ci = 0.95,
  rel.tol = .Machine$double.eps^0.3,
  logml_iter = 5000,
  silent_stan = TRUE,
  ...
)

Arguments

y

effect size per study. Can be provided as (1) a numeric vector, (2) the quoted or unquoted name of the variable in data, or (3) a formula to include discrete or continuous moderator variables.

SE

standard error of effect size for each study. Can be a numeric vector or the quoted or unquoted name of the variable in data

labels

optional: character values with study labels. Can be a character vector or the quoted or unquoted name of the variable in data

data

data frame containing the variables for effect size y, standard error SE, labels, and moderators per study.

d

prior distribution on the average effect size d. The prior probability density function is defined via prior.

tau

prior distribution on the between-study heterogeneity tau (i.e., the standard deviation of the study effect sizes dstudy in a random-effects meta-analysis. A (nonnegative) prior probability density function is defined via prior.

rscale_contin

scale parameter of the JZS prior for the continuous covariates.

rscale_discrete

scale parameter of the JZS prior for discrete moderators.

centering

whether continuous moderators are centered.

logml

how to estimate the log-marginal likelihood: either by numerical integration ("integrate") or by bridge sampling using MCMC/Stan samples ("stan"). To obtain high precision with logml="stan", many MCMC samples are required (e.g., logml_iter=10000, warmup=1000).

summarize

how to estimate parameter summaries (mean, median, SD, etc.): Either by numerical integration (summarize = "integrate") or based on MCMC/Stan samples (summarize = "stan").

ci

probability for the credibility/highest-density intervals.

rel.tol

relative tolerance used for numerical integration using integrate. Use rel.tol=.Machine$double.eps for maximal precision (however, this might be slow).

logml_iter

number of iterations (per chain) from the posterior distribution of d and tau. The samples are used for computing the marginal likelihood of the random-effects model with bridge sampling (if logml="stan") and for obtaining parameter estimates (if summarize="stan"). Note that the argument iter=2000 controls the number of iterations for estimation of the random-effect parameters per study in random-effects meta-analysis.

silent_stan

whether to suppress the Stan progress bar.

...

further arguments passed to rstan::sampling (see stanmodel-method-sampling). Relevant MCMC settings concern the number of warmup samples that are discarded (warmup=500), the total number of iterations per chain (iter=2000), the number of MCMC chains (chains=4), whether multiple cores should be used (cores=4), and control arguments that make the sampling in Stan more robust, for instance: control=list(adapt_delta=.97).

Examples

# \donttest{
### Bayesian Random-Effects Meta-Analysis (H1: d>0)
data(towels)
set.seed(123)
mr <- meta_random(logOR, SE, study,
  data = towels,
  d = prior("norm", c(mean = 0, sd = .3), lower = 0),
  tau = prior("invgamma", c(shape = 1, scale = 0.15))
)
mr
#> ### Bayesian Random-Effects Meta-Analysis ### 
#>    Prior on d:      'norm' (mean=0, sd=0.3) truncated to the interval [0,Inf]. 
#>    Prior on tau:    'invgamma' (shape=1, scale=0.15) with support on the interval [0,Inf]. 
#> 
#> # Bayes factors:
#>            (denominator)
#> (numerator) random_H0 random_H1
#>   random_H0      1.00     0.262
#>   random_H1      3.81     1.000
#> 
#> # Posterior summary statistics of random-effects model:
#>      mean    sd  2.5%   50% 97.5% hpd95_lower hpd95_upper  n_eff Rhat
#> d   0.196 0.088 0.032 0.194 0.373       0.015       0.349 5694.0    1
#> tau 0.129 0.087 0.033 0.106 0.355       0.022       0.299 4694.1    1
plot_posterior(mr)

# }
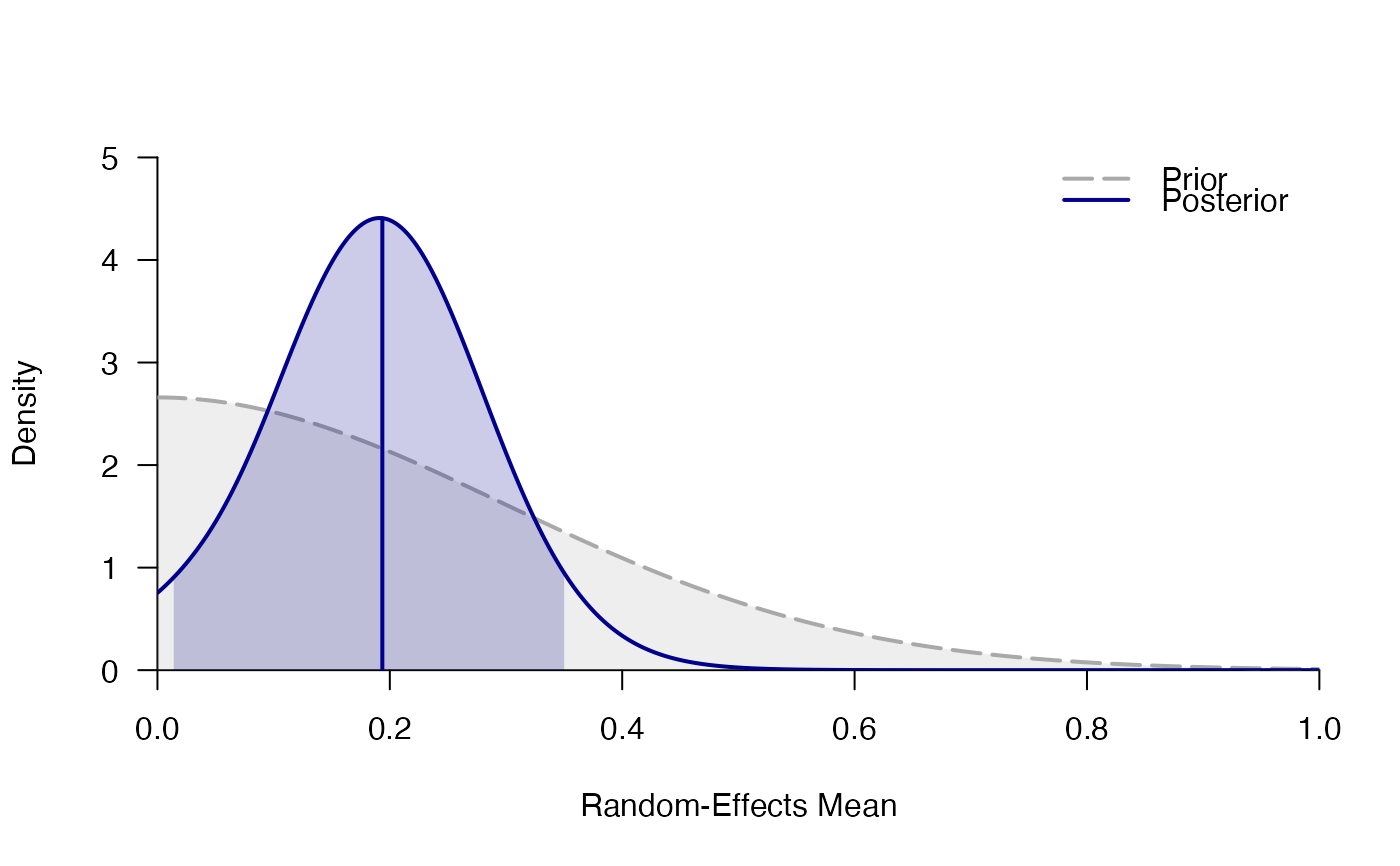